Fuerza Electromotriz Inducida en los Generadores Sincrónicos

Las Características principal de esta fuerza electromotriz son:

• Magnitud: se consigue relativamente fácil por medio de la regulación de la excitación.
• Frecuencia: se regula a través de la potencia activa o motor primario.
• Forma de la curva de variación: recordando que la fuerza electromotriz que alimenta las instalaciones industriales así como otros aparatos y maquinarias deben poseer una forma de curva con variación prácticamente sinusoidal.

Precisamente estos parámetros determinan la calidad de la energía generada. En el caso de que la forma de curva se aleje de la sinusoide, surgen los denominados armónicos superiores, que influyen de forma negativa sobre el propio generador, sobre las lineas de transmisión y sobre la mayoría de los consumidores. Los Armónicos superiores suelen provocar aumentos de perdidas. sobre tensiones en las lineas de transmisión y otras perturbaciones de orden secundaria. En ocasiones se toman en cuenta algunos detalles constructivos para que esta curva sea lo mas próximo a una sinusoide y evitar así los armónicos superiores.

Como reglas genéricas si la máquina tiene una construcción de polos salientes se toman en cuenta las siguientes precauciones:

• Se construyen de forma tal que en el entre hierro sea menor que:

$$ \delta < (0.5 a 2.0) \delta '$$

Delta → Entre hierro.

Delta prima → Entre hierro de las aristas del polo.

(imagen)

Máquina de polos interiores

(imagen)
Se construyen de forma tal que la parte que conforma el devanado ocupe un 75% de su paso polar (tau).

F.E.M. inducida en un conductor

Forma una curva con variación sinusoidal (no se tomaran en cuenta los armónicos superiores), Para obtener esta curva se colocara un conductor en el estator de la máquina. Esta se excita y se le da la rotación "n" constante/Sincrónica.

(imagen)

El valor instantáneo de la f.e.m. inducida en ese conductor es:

$$ e = B_x • l • v $$

e → f.e.m. inducida en el conductor.

l → Longitud del conductor.

v → Velocidad circunferencial lineal del rotor.

$ B_x $ → valor de la inducción magnética en el sitio donde esta el conductor para un instante dado donde e y v son constante y e variara como varia $ B_x. $ 

El valor eficaz de esa f.e.m. para un periodo completo (T) que naturalmente corresponde al periodo (2 tau) dos variaciones polares y suponiendo que la tensión en el conductor es:

$$ E{conductor} = \sqrt{ \frac {2} {T}  \int_0^\frac {2} {T} e_{conductor}^2 dt } $$

Por un lado la velocidad circunferencial lineal del rotor sera "v", recordando que: 

$$ \frac{\partial s}{\partial t} = R \frac{\partial  \theta }{\partial t} →  \omega \frac{D} {2} $$

$$ v= D \pi n$$

$$ 2 \pi n $$

$$ f = P n $$

Entonces:

$$ v = 2 \pi n \frac {D} {2} = D \pi n $$

Distribución polar ($ \tau $) $ = \frac {\pi D } { 2 P} $

$$ v = \frac {D \pi n} { 2P} * 2P = \frac {2 \pi D} { 2P} * P n = 2 \tau f = 2 \tau P $$

Factor de distribución de curva del campo (K_e):

$$ K_e = \frac {B} {B_{media}} $$

B → Inducción Eficaz

$ B_media $ → inducción media

$$ B= K_e * B_{media} $$

Para una sinusoide:

$$ K_e = \frac { \pi} {2 \sqrt {2}} $$

Flujo total para un polo ($ \varphi $)

$$ \varphi = \tau l B_{medio} $$

$$ E = B *l* v = 2 \tau f * l * K_e * B_{medio} $$

$$ E = 2 K_e \varphi f = 2 \frac { \pi } {2 \sqrt{2}} * \varphi * B_{medio} $$

$$ E = \frac { \pi } {\sqrt {2}} = 2.22 \varphi f $$

Si se tratara de un devanado completo y no un solo conductor para un devanado de paso completo esa fuerza electromotriz seria igual a dos veces la que hay en el conductor;

$$  E = 4.44 \varphi f $$

Y ademas puede aumentar "N" veces;

$$ E = 4.44 \varphi f N_c $$

$ N_c $ → Numero de conductores

F.E.M. inducida en un conductor pero para una distribución de campo sinusoidal

(Teniendo en cuenta los armónicos superiores)

Consideraciones:

1. Se considerara la inducción magnética simétrica con respecto al eje de abscisas y simétrico con respecto al eje del polo, para estos casos la curva de la inducción magnética contiene ademas del primer armónico o armónico fundamental, armónicos superiores de orden impar donde ese orden los vamos a organizar con la letra gamma.

(imagen)

Cada armónico determina con respecto a su armónico de flujo es decir que tendremos \varphi_gamma veces.

$$ \varphi_1 = \tau l B_{medio1} $$

$$ \varphi_3 = \frac{\tau}{3}  l B_{medio3} $$

$$ \varphi_5 = \frac{\tau}{5}  l B_{medio5} $$

$$ \varphi_{\wp} = \frac{\tau}{\wp}  l B_{medio \wp} $$

$$ K_e = \frac {B} {B_{medio}} = \frac {\pi}{2 \sqrt{2}} $$

$$ B = \frac {B_{max}} {\sqrt {2}} → (valor eficaz) $$

$$\frac {B_{max} /3} {B_{max}}= \frac {\pi}{2 \sqrt {2}} $$

$$B_{medio} = \frac {B_{max}}{\sqrt{2}} \frac {2 \sqrt{2}} {\pi}$$

$$ B_{medio} = \frac {2}{\pi} B_{max} $$

$$ \varphi_1 = \frac {2} {\pi} \tau l B_{max1} $$

$$ \varphi_3 = \frac {2} {\pi} \frac {\tau} {3} l B_{max3} $$

$$ \varphi_5 = \frac {2} {\pi} \frac {\tau} {5} l B_{max5} $$

$$ \varphi_{\wp} = \frac {2} {\pi} \frac {\tau} {\wp} l B_{max \wp} $$

Todos estos flujos de los diferentes armónicos giran con velocidad de rotación "n", es decir, velocidad del rotor de esa máquina sincrónica y por lo tanto la frecuencia va a variar para cada uno de sus armónicos;

$$ f_1 = P n; f_3 = 3 P n; f_5 = 5 P n; \cdots f_{\wp} = \wp P n $$

$$ E_{conductor1} = \frac {\pi}{\sqrt{2}} \varphi_1 f_1 = \frac {\pi} {\sqrt {2}} ( \frac {2}{\pi} \tau l B_{max1} ) f_1 → E_{conductor1} = \sqrt {2} \tau l B_{max1} f_1 $$

$$ E_{conductor3} =\frac {\pi}{\sqrt{2}} \varphi_3 f_3 = \sqrt {2} \tau l B_{max} f_1 $$

$$ E_{conductor5} = \frac {\pi}{\sqrt{2}} \varphi_5 f_5 = \sqrt {2} \tau l B_{max} f_1 $$

$ E_{conductor \wp} = \frac {\pi}{\sqrt{2}} \varphi_{\wp} f_{\wp} = \sqrt {2} \tau l B_{max} f_1 $

El valor eficaz de la fuerza electromotriz resultante en el conductor será:

$$ E_{conductor} = \sqrt {E_{conductor1}^2 + E_{conductor3}^2 + E_{conductor5}^2 + \cdots + E_{conductor \wp}^2} $$

$$ E_{conductor} = E_{conductor1} \sqrt { 1 + (\frac {E_{conductor3}}{E_{conductor1}})^2 + (\frac {E_{conductor5}}{E_{conductor1}})^2 + \cdots +(\frac {E_{conductor \wp}}{E_{conductor1}})^2} $$

$$ E_{conductor} = E_{conductor1} \sqrt { 1 + (\frac {E_{max3}}{E_{max1}})^2 + (\frac {E_{max5}}{E_{max1}})^2 + \cdots +(\frac {E_{max \wp}}{E_{max1}})^2} $$

$$ E_{conductor} = \frac {\pi} {\sqrt {2}} \varphi_1 f_1 \sqrt {1+ K_{B3}^2 + K_{B5}^2 + \cdots + K_{B \wp}^2} $$

Donde:

$$ K_{B3}= \frac {B_max3} {B_max1}; K_{B5}= \frac {B_max5} {B_max1}; K_{B \wp}= \frac {B_max \wp} {B_max1} $$

Estos coeficientes K_B3, K_B5, etcétera representan relaciones de las amplitudes de los armónicos superiores de inducción máxima sobe la amplitud de la inducción máxima sobre la amplitud de la inducción máxima correspondiente al primer amónico u onda fundamental.

Como el flujo de una semi-onda de inducción del armónico fundamental se le añade o se le resta al flujo de una semi-onda del campo del armónico superior entonces, el flujo total por cada polo se expresa por la siguiente suma algebraica;

$$ \varphi = \varphi_1 \pm \varphi_3 \pm \varphi_5 \pm \cdots \pm \varphi_{\wp} $$

$$ \varphi = \varphi_1 ( 1 \pm \frac {\varphi_3}{\varphi_1} \pm \frac {\varphi_5}{\varphi_1} \pm \cdots \pm \frac {\varphi_{\wp}}{\varphi_1}) $$

$$ \varphi = \varphi_1 ( 1 \pm \frac {\varphi_{max3}}{\varphi_{max1}} \pm \frac {\varphi_{max5}}{\varphi_{max1}} \pm \cdots \pm \frac {\varphi_{max \wp}}{\varphi_{max1}}) $$

$$ \varphi = \varphi_1 \underbrace{( 1 \pm \frac{K_{B3}}{3} \pm \frac{K_{B5}}{5} \pm \cdots \pm \frac{K_{B \wp}}{\wp})} $$

$$K_f → Factor de forma de campo $$

$$ \varphi = \varphi_1 K_f → \varphi_1 \simeq \frac {\varphi }{K_f} $$

Ahora podemos deducir esta ecuación:

$$ E_{conductor} = \frac {\pi}{\sqrt{2}} \varphi f \frac {\sqrt {1+ K_{B3}^2 + K_{B5}^2 + \cdots + K_{B \wp}^2}} {1 \pm \frac{K_{B3}}{3} \pm \frac{K_{B5}}{5} \pm \cdots \pm \frac{K_{B \wp}}{\wp}} $$

De esta expresión se deduce que aunque se hayan tomado en cuenta los armónicos superiores estos influyen relativamente poco en el valor o magnitud de la fuerza electromotriz inducida en el conductor pero si influyen sobre la forma de la curva de la fuerza electromotriz inducida en el conductor afectandola de forma directa y deformandola significativamente.

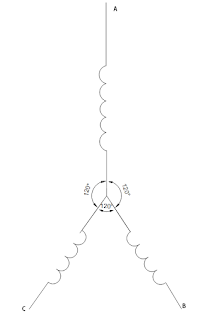
F.E.M. inducida en una espira de devanado de paso entero (y = \tau)

(imagen)

La fuerza electromotriz inducida para la espira se obtiene como la resta geometrica de "$ E'_{conductor} $" y "$ E''_{conductor} $" inducida en cada conductor de la espira, es decir 1' y 1'' respectivamente por lo tanto el valor eficaz de la fuerza electromotriz de una espira de paso entero sera igual a 2 veces la del conductor.

Generalizando para una bobina conectada en serie con "N" cantidad de espiras. Esa fuerza electromotriz inducida en el conductor sera igual a

$$ E = 2 N E_{conductor} = \frac {2 \pi} { \sqrt{2}} \varphi f \frac {\sqrt {1+ K_{B3}^2 + K_{B5}^2 + \cdots + K_{B \wp}^2}} {1 \pm \frac{K_{B3}}{3} \pm \frac{K_{B5}}{5} \pm \cdots \pm \frac{K_{B \wp}}{\wp}} $$

Simplificado: $ E = 4.44 \varphi N f_1 $

Fuerzas Magnetizantes para devanados de corriente alterna

Distribución de la inducción  magnética en el entre-hierro de la máquina

El campo magnético del devanado de una máquina de corriente alterna depende de:

1. La corriente que por el circule.
2. La disposición de los conductores del devanado.
3. La configuración del circuito magnético de la máquina.
4. Las propiedades magnéticas de cada uno de sus sectores.

La distribución de la inducción magnética a lo largo del entre-hierro de la máquina dependerá de:

1. Magnitudes y formas de las fuerzas electromotrices que se inducen en esos devanados.
2. La magnitud y carácter de los esfuerzos electromagnéticos que surgen y crean los momentos de rotación de la máquina.

Fuerza Magnetizante y curva de inducción magnética en el entre-hierro de una bobina

Este estudio se realiza para una bobina de paso entero una máquina bipolar que posea un entre-hierro uniforme.

(imagen)

En cuanto a la curva de la distribución de la inducción magnética del entre-hierro se adopta la curva de trazo. La concavidad de la curva de trazo se explica por el efecto de permeabilidad magnética final del acero.

Si se asume una permeabilidad magnética para el acero de que;

$$  \mu  = \infty  $$

Y ademas si se desprecian las distorsiones del campo magnético de los conductores de la bobina, entonces la distribución de la inducción magnética en el entre-hierro se adopta como una forma de onda rectangular.

Valor de la inducción magnética en el entre-hierro

$$H\to Ni$$