Característica angular del generador sincrónico

La potencia de la máquina sincrónica  generalmente se expresa en función de los parámetros eléctricos que se miden a la salida del estator del generador sincrónico y en sentido general:

$ P = m*U*I*Cos (\varphi) $

Al analizar los problemas relacionados con el trabajo en paralelo de las máquinas con las redes se acostumbra a hacer el siguiente análisis.

$ P = f(E_0, U, \theta) $

$E_0$ → Tensión a la salida

$U$ → Tensión Generada

$\theta$ → Angulo entre $E_0$ y $U$ determinado por la posición angular del rotor con respecto al flujo magnético giratorio resultante en el estator.

Características angular de las máquinas sincrónicas

$ P = f(\theta) $

Para: $ U = $ constante, $E_0 =$ constante, $f =$ constante.

Para obtener esta variación utilizaremos el diagrama vectorial de blondel para un generador de polos salientes considerando la resistencia activa del devanado del estator nula la cual es considerablemente menor a su inductancia.

$$ r_a \simeq 0 $$

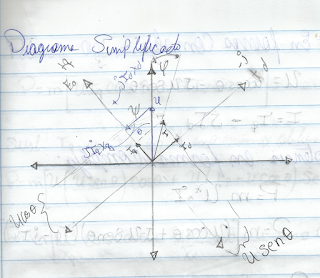
Diagrama simplificado

Si proyectamos las tensiones y las fuerzas electromotrices inducidas sobre las direcciones de los ejes longitudinales y transversales se obtiene lo siguiente:

$ E_0 = U cos (\theta) + I_d X_d $

$ 0 = U sen (\theta) - I_q X_q $

$ I_d = \frac { -U Cos (\theta) + E_0}{X_d} $

$ I_q = \frac {U Sen (\theta)} { X_q} $

En forma compleja:

$$ U = u Cos (\theta) - j(u Sen (\theta) $$

$$ I = I_q - j (I_d) $$

Potencia en forma compleja:

$$ P = m*U^\star *I $$

$$ P = m[(U Cos \theta + j(U Sen \theta)(I_q - j I_d)] $$

$$ P = m [U I_q Cos \theta + j U I_q sen \theta - j U I_d Cos \theta + U I_d Sen \theta] $$

$$ P = m [U I_q Cos \theta + U I_d Sen \theta] - j m[U I_d Cos \theta - U I_q Sen \theta ] $$

La parte real determina la potencia activa de la máquina.

Potencia activa:

$$ P = m [U I_q Cos \theta + U I_d Sen \theta] $$

Sustituyendo I_q y I_d en la expresión se obtiene:

$ P = m[ U(\frac { U Sen \theta} {X_q} ) Cos \theta + U ( \frac {E_0 - U cos \theta}{X_d}) Sen \theta] $

$ P= m [\frac{U^2}{X_q} Sen \theta Cos \theta + \frac {U E_0} {X_d} Sen \theta - \frac {U^2} {X_d} Sen \theta Cos \theta] $

$ P = m \frac {U E_0} {X_d} Sen \theta + \frac {m U^2}{2} (\frac {1} {X_q} - \frac {1}{X_d} Sen 2 \theta $

$P_e$ → Componente fundamental de la potencia de un generador.

$ P_e = \frac { m U E_0}{X_d} Sen \theta $

$P_U$ → Componente suplementaria de la potencia del generador

$P_U = \frac {m U^2}{2} (\frac {1}{X_q} - \frac {1}{X_d}) Sen 2 \theta $

Observaciones

• Cuando no existe la excitación: $E_0 = 0$
• Para un generador de polos salientes: $X_q \neq X_d$
• Para un generador de polos interiores $ X_d = X_q $

Por lo tanto $ P_U = 0 $

$ P = P_e = m \frac {E_0 U}{X_d} Sen \theta $

• Para polos salientes $ P = P_e + P_u $
• Para $r_a = 0$ Pero $ X_d $ y $X_q$ constantes:  U y $ E_0$ son constantes.

Ahora después de estas demostraciones podemos obtener la gráfica de la característica angular.

Gráfica de la característica angular del generador sincrónico

Para una máquina de:

• Polos interiores se obtiene la potencia máxima cuando $ \theta = \frac {\pi}{2}$ .
• Polos salientes se obtiene la potencia máxima para $\theta < \frac {\pi}{2}$.
• Para otros valores de $ \theta $.

$P(+)$ → $ 0< \theta < \pi $; $ 2\pi < \theta < 3\phi $; etc...

$P(-)$ → $ -\pi < \theta < 0$; $ \pi < \theta < 2 \pi $; etc...

La potencia positiva corresponde a los regímenes de funcionamiento del generador, entregando energía eléctrica al sistema.

La potencia negativa corresponde a los regímenes de funcionamiento de motor, es decir, consumiendo una energía del sistema.

Sí el motor girara a una velocidad no sincrónica, es decir, que saliera de sincronismo, el angulo $\theta$ variaría continuamente para velocidad mayor que la sincrónica $\theta$ crecería continuamente y la máquina pasa consecutivamente de régimen de generador a régimen de motor y viceversa.

Potencia y momento electromagnético

Se denomina potencia electromagnética a la potencia transmitida por vía electromagnética desde el rotor del generador sincrónico al estator a través del campo magnético que atraviesa el entre-hierro.

Una parte pequeña de esta potencia se disipa en cubrir las perdidas en el acero del generador o perdidas magnéticas y la parte restante se convierte en potencia eléctrica en el devanado del estator, entendiendo se por potencia electromagnética solo la parte que se convierte en potencia eléctrica en el devanado del estator.

Bajo estas condiciones y manteniendo la resistencia activa del devanado del estator nulas, es decir, que no hay perdidas eléctricas en este devanado, entonces la potencia electromagnética sera igual a la potencia eléctrica que el generador suministra al sistema.

$ P_{e.m.} = \frac {m E_0 U}{X_d} Sen \theta + \frac {m U^2} {2}(\frac{1}{X_q} - \frac{1}{X_d}) Sen 2\theta $

Ya el generador con carga eléctrica actúa lo que se denomina momento electromagnético como un par de frenado sobre el rotor, y se determina a través de la potencia electromagnética y la velocidad angular mecánica de rotación ($\omega$).

$ M_{e.m.} = \frac{P_{e.m.}}{\omega} $

$ M_{e.m.} = m \frac{E_0 U}{\omega X_d} Sen \theta + \frac {m U^2} {2\omega}(\frac {1}{X_q} - \frac{1}{X_d}) Sen 2\theta $

En el régimen de motor el momento electromagnético cambia de signo deja de ser un par de frenado y actúa sobre el rotor pero en el sentido de su rotación.

Para máquinas de polos salientes

$M_{e.m} = M_{e.m (e)} +  M_{e.m (u)} $

Donde:

$ M_{e.m (e)} = m \frac { E_0 U} {\omega X_d} Sen \theta $

$ M_{e.m (u)} = \frac {m U^2} { 2 \omega} (\frac {1}{X_q} - \frac {1}{X_d}) Sen 2\theta $

Sobre-excitación y sub-excitación del generador sincrónico

Sobre-excitación ( $ 0 < \Phi < \frac{\pi}{2}) ( r_a \simeq 0) $

Sub-excitación (  $ 0 > \Phi > \frac{\pi}{2} $ )

Característica en forma de "V" del generador sincrónico

Esta característica representa la forma en que varia la corriente de carga del estator para variación de la corriente de excitación si se mantiene constante la tensión a la salida la potencia a la salida y la velocidad de rotación.

Esta característica muestra que para cualquier carga del generador existe un valor de la corriente de excitación para el cual la corriente del estator es mínima e igual solo a su componente activa ( $I Cos \varphi$ ), en el cual el generador trabaja con un factor de potencia unidad, indicando la linea de punto en la gráfica la corriente de excitación para un factor de potencia unidad.

Para diferentes cargas $P_1$, $P_2$, $P_3$, cuando esta carga aumenta, aumenta la corriente de excitación y la curva se inclina para compensar las caídas de tensiones activas, sin embargo, el generador trabaja normalmente en un régimen sobre-excitado.